Acerca de parábolas: física, astronomía y literatura
Hoy quisiera hablarles de la parábola bajo todos sus aspectos: literario, matemático y físico. Para dejar las cosas claras, empecemos con la definición de "parábola" según la Real Academia Española:
1. f. Narración de un suceso fingido de que se deduce, por comparación o semejanza, una verdad importante o una enseñanza moral.
2. f. Geom. Curva abierta cuyos puntos son equidistantes de una recta y un punto fijos, formada por dos ramas simétricas respecto de un eje, y que resulta de cortar un cono circular recto con un plano paralelo a una generatriz.
A mi gusto estas definiciones no revelan la belleza de la parábola que se esconde bajo sus múltiples apariencias. Claramente la primera acepción tiene que ver con la figura literaria llamada parábola y la segunda es su definición matemática (aunque no sea la única). Lo que es quizás un poco sorprendente es que no se haga ninguna referencia al uso que se le da en el campo de la física y de la astronomía. Es cierto que no es el objetivo del diccionario (a menos que sea enciclopédico) pero aún así no deja de sorprenderme. Pero vamos por partes...
Con respecto a la figura literaria, los textos sagrados y las enseñanzas religiosas suelen usar este recurso de manera repetida y casi abusiva. El Nuevo Testamento está plagado de ejemplos donde Jesucristo inculca valores morales a través de historias de las cuales sus auditores pueden extraer una moraleja o una conducta piadosa a seguir (bajo pena de recibir un castigo divino si se portan mal...). Una de las más famosas quizás es la parábola del sembrador cuya interpretación le ha dado mucho que hablar a los estudiosos. En breve, un sembrador salió al campo y sus semillas cayeron en 4 lugares distintos: junto al camino, sobre la roca, en medio de los espinos y en tierra buena. Sólo las que cayeron en tierra buena produjeron cosecha. En este caso, el sembrador representa al creyente que predica la palabra divina (siembra la semilla) y los 4 ambientes son los diferentes tipos de personas según su grado de aceptación y conversión. No deseo entrar en discusiones religiosas, era simplemente para ilustrar la acepción 1).
 Sin embargo, no es para nada obvia la conexión entre esta figura literaria y la parábola matemática. Si apelamos a la etimología, podemos obtener algunos elementos de respuesta. Resulta que parábola proviene de la palabra griega παραβολη: "pará" significa "al margen" y "bolé" significa "arrojar" o "lanzar". Yuxtapuestas estas dos palabras obtenemos "arrojar al margen" que significa "comparar". Ahora bien, ¿qué tiene que ver esto con la definición matemática? Si miran bien la acepción 2), verán que se habla de puntos equidistantes de una recta y un punto fijo. Por lo tanto, el conjunto de puntos que verifican esa condición forma una parábola. Dicho de otro modo y usando la figura de acá al lado, si comparamos la distancia de un punto dado de la parábola (por ejemplo P, Q, R o S) al punto focal F y la comparamos con la distancia a la recta debajo obtenemos que son iguales.
Sin embargo, no es para nada obvia la conexión entre esta figura literaria y la parábola matemática. Si apelamos a la etimología, podemos obtener algunos elementos de respuesta. Resulta que parábola proviene de la palabra griega παραβολη: "pará" significa "al margen" y "bolé" significa "arrojar" o "lanzar". Yuxtapuestas estas dos palabras obtenemos "arrojar al margen" que significa "comparar". Ahora bien, ¿qué tiene que ver esto con la definición matemática? Si miran bien la acepción 2), verán que se habla de puntos equidistantes de una recta y un punto fijo. Por lo tanto, el conjunto de puntos que verifican esa condición forma una parábola. Dicho de otro modo y usando la figura de acá al lado, si comparamos la distancia de un punto dado de la parábola (por ejemplo P, Q, R o S) al punto focal F y la comparamos con la distancia a la recta debajo obtenemos que son iguales.
 Personalmente, me parece mucho más bonita la segunda parte de la definición donde se habla de secciones de un cono circular recto. Una imagen vale más que mil palabras :-) Como pueden ver al lado, si uno corta con un plano el cono en diferentes lugares se pueden obtener diferentes secciones cónicas:
Personalmente, me parece mucho más bonita la segunda parte de la definición donde se habla de secciones de un cono circular recto. Una imagen vale más que mil palabras :-) Como pueden ver al lado, si uno corta con un plano el cono en diferentes lugares se pueden obtener diferentes secciones cónicas:
- si elegimos un plano paralelo a la base se obtiene un círculo (en rojo),
- si inclinamos ligeramente este plano se obtiene una elipse (en verde),
- inclinando aun más el plano, si éste atraviesa la base del cono y la línea de intersección se encuentra en el hemisferio izquierdo del cono, entonces obtenemos una parábola (en azul),
- finalmente si seguimos inclinando el plano hasta que la línea de intersección entre el plano y la base del cono esté en el hemisferio derecho del cono, entonces se obtiene una hipérbola. ¡Estas curvas o secciones cónicas son una verdadera belleza!
Abordemos el último aspecto de la parábola: su importancia en el campo de la física y sus aplicaciones en astronomía. La parábola surge de manera natural de las leyes de Newton cuando se considera por ejemplo la caída de un cuerpo en un campo gravitatorio. Es un ejercicio de mecánica archi-clásico calcular la trayectoria de una pelotita que se lanza con una cierta velocidad y con un cierto ángulo hacia arriba. Si se desprecia el rozamiento con el aire, la pelotita dibuja una parábola abierta hacia abajo y cuya forma depende de la posición y velocidad iniciales.
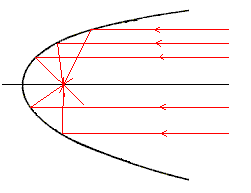 Para concluir, en astronomía, se usan las parábolas para observar el cielo. Si uno tiene una serie de rayos de luz (paralelos ya que vienen de muy lejos) que chocan la cara interior (reflectora) de la parábola, éstos convergen en un sólo punto (el punto focal). Esto se debe a las propiedades geométricas de la parábola. Ahora bien, esto se puede usar para concentrar señales luminosas: si se aumenta la superficie de la antena parabólica entonces se aumentará la intensidad. Esta técnica se usa en la construcción de telescopios donde se coloca un receptor o cámara en el punto focal como pueden ver acá abajo. Este principio básico es realmente uno de los pilares de la astronomía moderna.
Para concluir, en astronomía, se usan las parábolas para observar el cielo. Si uno tiene una serie de rayos de luz (paralelos ya que vienen de muy lejos) que chocan la cara interior (reflectora) de la parábola, éstos convergen en un sólo punto (el punto focal). Esto se debe a las propiedades geométricas de la parábola. Ahora bien, esto se puede usar para concentrar señales luminosas: si se aumenta la superficie de la antena parabólica entonces se aumentará la intensidad. Esta técnica se usa en la construcción de telescopios donde se coloca un receptor o cámara en el punto focal como pueden ver acá abajo. Este principio básico es realmente uno de los pilares de la astronomía moderna.
Como verán las parábolas no conocen fronteras dado su uso literario, matemático, físico, astronómico y tecnológico. Espero que la próxima vez que vean o dibujen una parábola aprecien su belleza plurifacética :-)
¡Saludos parabólicos!
1. f. Narración de un suceso fingido de que se deduce, por comparación o semejanza, una verdad importante o una enseñanza moral.
2. f. Geom. Curva abierta cuyos puntos son equidistantes de una recta y un punto fijos, formada por dos ramas simétricas respecto de un eje, y que resulta de cortar un cono circular recto con un plano paralelo a una generatriz.
A mi gusto estas definiciones no revelan la belleza de la parábola que se esconde bajo sus múltiples apariencias. Claramente la primera acepción tiene que ver con la figura literaria llamada parábola y la segunda es su definición matemática (aunque no sea la única). Lo que es quizás un poco sorprendente es que no se haga ninguna referencia al uso que se le da en el campo de la física y de la astronomía. Es cierto que no es el objetivo del diccionario (a menos que sea enciclopédico) pero aún así no deja de sorprenderme. Pero vamos por partes...
Con respecto a la figura literaria, los textos sagrados y las enseñanzas religiosas suelen usar este recurso de manera repetida y casi abusiva. El Nuevo Testamento está plagado de ejemplos donde Jesucristo inculca valores morales a través de historias de las cuales sus auditores pueden extraer una moraleja o una conducta piadosa a seguir (bajo pena de recibir un castigo divino si se portan mal...). Una de las más famosas quizás es la parábola del sembrador cuya interpretación le ha dado mucho que hablar a los estudiosos. En breve, un sembrador salió al campo y sus semillas cayeron en 4 lugares distintos: junto al camino, sobre la roca, en medio de los espinos y en tierra buena. Sólo las que cayeron en tierra buena produjeron cosecha. En este caso, el sembrador representa al creyente que predica la palabra divina (siembra la semilla) y los 4 ambientes son los diferentes tipos de personas según su grado de aceptación y conversión. No deseo entrar en discusiones religiosas, era simplemente para ilustrar la acepción 1).
 |
| Fuente: Wikimedia Commons, Dnalor_01, licencia CC-BY-SA 3.0 Hortus Deliciarum, Hortus Deliciarum circa 1180. |
 Sin embargo, no es para nada obvia la conexión entre esta figura literaria y la parábola matemática. Si apelamos a la etimología, podemos obtener algunos elementos de respuesta. Resulta que parábola proviene de la palabra griega παραβολη: "pará" significa "al margen" y "bolé" significa "arrojar" o "lanzar". Yuxtapuestas estas dos palabras obtenemos "arrojar al margen" que significa "comparar". Ahora bien, ¿qué tiene que ver esto con la definición matemática? Si miran bien la acepción 2), verán que se habla de puntos equidistantes de una recta y un punto fijo. Por lo tanto, el conjunto de puntos que verifican esa condición forma una parábola. Dicho de otro modo y usando la figura de acá al lado, si comparamos la distancia de un punto dado de la parábola (por ejemplo P, Q, R o S) al punto focal F y la comparamos con la distancia a la recta debajo obtenemos que son iguales.
Sin embargo, no es para nada obvia la conexión entre esta figura literaria y la parábola matemática. Si apelamos a la etimología, podemos obtener algunos elementos de respuesta. Resulta que parábola proviene de la palabra griega παραβολη: "pará" significa "al margen" y "bolé" significa "arrojar" o "lanzar". Yuxtapuestas estas dos palabras obtenemos "arrojar al margen" que significa "comparar". Ahora bien, ¿qué tiene que ver esto con la definición matemática? Si miran bien la acepción 2), verán que se habla de puntos equidistantes de una recta y un punto fijo. Por lo tanto, el conjunto de puntos que verifican esa condición forma una parábola. Dicho de otro modo y usando la figura de acá al lado, si comparamos la distancia de un punto dado de la parábola (por ejemplo P, Q, R o S) al punto focal F y la comparamos con la distancia a la recta debajo obtenemos que son iguales. Personalmente, me parece mucho más bonita la segunda parte de la definición donde se habla de secciones de un cono circular recto. Una imagen vale más que mil palabras :-) Como pueden ver al lado, si uno corta con un plano el cono en diferentes lugares se pueden obtener diferentes secciones cónicas:
Personalmente, me parece mucho más bonita la segunda parte de la definición donde se habla de secciones de un cono circular recto. Una imagen vale más que mil palabras :-) Como pueden ver al lado, si uno corta con un plano el cono en diferentes lugares se pueden obtener diferentes secciones cónicas:- si elegimos un plano paralelo a la base se obtiene un círculo (en rojo),
- si inclinamos ligeramente este plano se obtiene una elipse (en verde),
- inclinando aun más el plano, si éste atraviesa la base del cono y la línea de intersección se encuentra en el hemisferio izquierdo del cono, entonces obtenemos una parábola (en azul),
- finalmente si seguimos inclinando el plano hasta que la línea de intersección entre el plano y la base del cono esté en el hemisferio derecho del cono, entonces se obtiene una hipérbola. ¡Estas curvas o secciones cónicas son una verdadera belleza!
 Para concluir, en astronomía, se usan las parábolas para observar el cielo. Si uno tiene una serie de rayos de luz (paralelos ya que vienen de muy lejos) que chocan la cara interior (reflectora) de la parábola, éstos convergen en un sólo punto (el punto focal). Esto se debe a las propiedades geométricas de la parábola. Ahora bien, esto se puede usar para concentrar señales luminosas: si se aumenta la superficie de la antena parabólica entonces se aumentará la intensidad. Esta técnica se usa en la construcción de telescopios donde se coloca un receptor o cámara en el punto focal como pueden ver acá abajo. Este principio básico es realmente uno de los pilares de la astronomía moderna.
Para concluir, en astronomía, se usan las parábolas para observar el cielo. Si uno tiene una serie de rayos de luz (paralelos ya que vienen de muy lejos) que chocan la cara interior (reflectora) de la parábola, éstos convergen en un sólo punto (el punto focal). Esto se debe a las propiedades geométricas de la parábola. Ahora bien, esto se puede usar para concentrar señales luminosas: si se aumenta la superficie de la antena parabólica entonces se aumentará la intensidad. Esta técnica se usa en la construcción de telescopios donde se coloca un receptor o cámara en el punto focal como pueden ver acá abajo. Este principio básico es realmente uno de los pilares de la astronomía moderna. |
| Fuente: Wikipedia (Richard Bartz) |
¡Saludos parabólicos!
Excelente mente grandísima percepción pero reflexiva apreciación de nuestra casa.
ResponderBorrarMe alegro de que haya apreciado la nota. ¡Saludos!
Borrar¿QUIERES VER A DIOS?
ResponderBorrar¡LEE ESTO!
Las tres cosas que te alejan y
Las tres que te acercan a Dios
- El exceso de alcohol te aleja de Dios
- El exceso de drogas te aleja de Dios
- El exceso de sexo sin amor también te aleja de Dios
Las tres que te acercan a Dios
- Ama a tu prójimo como a tí mismo
- Aprende a perdonar y
- A ser humilde
Eternamente
Joaquín Gorreta Martínez 62 años
Hipérbole y elipse también están relacionadas en la matemática y la literatura
ResponderBorrar